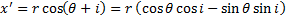Equation of Circle in 3D and Snap Tangent

For a time I was on a bit of an AutoCAD like calculation kick and went through some interesting calculations like snap tangent, snap perpendicular, and intersection of a line with a plane. I wanted to take the next step on snap tangent and consider snap tangent to a sphere.

Snap tangent means, start with some point and try to find a point on the destination object (circle, sphere, ellipse, anything) that causes the line segment between the first point and the second point to be tangent to the object selected. My post about snap tangent, showed the result for a circle and worked in 2D. If you get the concept in 2D and are ready to take the concept to 3D for a sphere, you probably recognize without proof that the set of possible points on the sphere which will result in a tangential point, forms a circle. You can pretty much mentally extrapolate from the following picture which a repeat from the previous post.

Fig. 1 - Can you imagine the snap tangent circle on this if we allow the figure to represent a sphere? The snap tangent circle has center \(E\) and radius \(a\).

I will not repeat the method of calculation from the previous post but will simply observe that we can produce the values \(E\) and \(a\), which are the center and radius of the snap tangent circle. We add to this the normal of this circle, \(N = A - C\), and then normalize \(N\).

So, now we need a way to describe this circle which is not too onerous. A parametric vector equation is the simplest expression of it. We take our inspiration from the classic representation of circles in parametric form, which is
\[ p(\theta) = (x(\theta), y(\theta)) \] \[ x(\theta) = r \cos{\theta} \] \[ y(\theta) = r \sin{\theta}. \]
We have a normal from which to work from, but we need to have an entire coordinate system to work with. The classic parametric equations have everything in a neat coordinate system, but to describe a circle that's oriented any which way, we need to cook up a coordinate system to describe it with. Observe a change to the foregoing presentation that we can make:
\[ p(\theta) = r \cos{\theta} (1, 0) + r \sin{\theta} (0, 1) = r \cos{\theta} \vec{x} + r \sin{\theta} \vec{y}\]
The normal vector we have is basically the z-axis of the impromptu coordinate system we require, but we don't have a natural x-axis or y-axis. The trouble is there are an infinite number of x-axes that we could choose, we just need something perpendicular to \(N = (n_x, n_y, n_z).\) So, let's just pick one. If I take the cross product between \(N\) and any other vector that isn't parallel to \(N\), I will obtain a value which is perpendicular to \(N\) and it can serve as my impromptu x-axis. To ensure I don't have a vector which is close to the direction of \(N\), I will grab the basis vector, which is the most "out of line" with the direction of \(N\). So, for example (F# style),

        let b = if abs(normal.[0]) <= abs(normal.[1]) then    
                    if abs(normal.[0]) <= abs(normal.[2]) then
                        DenseVector([| 1.0; 0.0; 0.0 |])
                    else
                        DenseVector([| 0.0; 0.0; 1.0 |])
                else
                    if abs(normal.[1]) <= abs(normal.[2]) then
                        DenseVector([| 0.0; 1.0; 0.0 |])
                    else
                        DenseVector([| 0.0; 0.0; 1.0 |])

In this case, I have 

\[\vec{x} = b \times N\] \[\vec{y} = N \times \vec{x}.\]

Using this impromptu coordinate system, I can express an arbitrary circle in parametric form, having center \(C\) and radius \(r\) as

\[ p(\theta) = C + \vec{x} r \cos{\theta} + \vec{y} r \sin{\theta}.\]

Thus, our snap tangent circle is given from above as 

\[ p(\theta) = E + \vec{x} a \cos{\theta} + \vec{y} a \sin{\theta},\]

where we would use \(N = A - C\) (normalized) to be the beginning of our coordinate system.

Plotting a LWPOLYLINE in Maxima

In this post, I want to show how to produce a representation of LWPOLYLINEs in Maxima that is suitable for plotting to the plot2d function. The direct usefulness of such an operation is dubious. Think of this as a worked example to help build understanding of a few mathematical and computing tools.

Recap
The LWPOLYLINE is a 2d representation of polylines that represents each vertex as having x-value, y-value, and bulge value. The bulge value indicates the path of travel from the current point to the next one. Either it will go straight (bulge = 0), veer to the left and back as a CW arc (bulge < 0), or it will veer to the right and back as a CCW arc (bulge > 0).

So, it will

• bulge left (< 0),
• go straight (= 0), or
• bulge right (> 0).

More details on the mathematics of the bulge factor can be found here and here.

The Pieces

First of all, we define our problem and break its solution up into pieces. A polyline is of such a nature that is does not make a good "\(f(x)\)" type function (plotting \(y\) versus \(x\)). However, it lends itself to parametric expression well enough. So, we will have an \(x(s)\) function and a \(y(s)\) function. Ideally, I would like to specify a length along the polyline (measured from the start) and get a point \((x(s), y(s))\). (If you have a surveying background, think \(s = \) station number.)

So, I need to have parametric equations for lines and for arcs that are parameterized for arc length and initial value of the parameter. I then need to stitch these together to make both an \(x\) and a \(y\) piecewise function.

Linear

Parametric equations for lines involve a direction and a starting point. Simply normalize the direction vector to parameterize for length. This looks like

\[(x(s), y(s)) = A + \frac{(B-A)}{||B-A||}s,\]

where \(A\) is the starting point and \(B\) is the final point. We will need to adjust the initial value to account for all of the length of the polyline prior to the initial point on this segment, say, \(s_i\) which changes our equations to

\[(x(s), y(s)) = A + \frac{(B-A)}{||B-A||}(s-s_i).\]

Arc

Parametric equations for arcs use a center, radius, initial angle, direction of rotation, and total angle subtended (some variation of feasible input parameters admitted). Parameterizing for arc length isn't as obvious as it was for lines, so let's start with a basic circle:

\[x(s) = c_x + r \cos{s}\]

\[y(s) = c_y + r \sin{s},\]

where \((c_x, c_y)\) is the center and \(r\) is the radius of the circle. For our reparameterization to work we require that radian measure be used (or else require degrees and do the conversion in the function, but why make work for ourselves and introduce inefficiency?). Recall that the definition of radians is the ratio of arc length to radius (\(\theta = s/r\)). So, our parameter becomes \(s/r\) and so we have

\[x(s) = c_x + r \cos{\left(\frac{s}{r}\right)}\]

\[y(s) = c_y + r \sin{\left(\frac{s}{r}\right)}.\]

To get the right starting point for our function we need the parameter inside the trig functions to be equal to the correct initial angle when the input value of \(s_i\) (length of polyline so up to the start of the arc) is given. We need, then, the initial angle, say \(\theta_i\), plus the angle past initial that the given \(s\) corresponds to. Thus,

\[x(s) = c_x + r \cos{\left(\theta_i + \sigma \frac{s-s_i}{r}\right)}\]

\[y(s) = c_y + r \sin{\left(\theta_i + \sigma \frac{s-s_i}{r}\right)},\]

where \(\sigma\) is 1 or -1 as per the sign of the bulge factor.

Piecewise

Making a piecewise function parameterized for length requires that we keep track of the length of the polyline up to the segment we are about to address. Implementing it in Maxima also requires a bit of acquaintance with the methods available to us for doing so. It is possible to use if-then-else logic to achieve this and obtain something that works fine for plotting purposes. As an example of this, consider a really simple example:

f(x) := if x < 1 then x^2 else x^3;

plot2d(f(x),[x,-1,2]);

Fig 1. If-then-else logic in functions plots fine.

There's another, somewhat handier approach to this problem, namely, the characteristic function. The characteristic function function is a way of expressing conditions as multiplication by 1 or 0 in order to include and exclude the appropriate expression. charfun2(x,a,b) returns 1 if \(x\in [a,b)\), else 0. So, we can modify the above function to be as follows and obtain the same result. 

load(interpol);

f(x) := charfun2(x,-inf,1)*x^2 + charfun2(x,1,inf)*x^3;
plot2d(f(x),[x,-1,2]);

One nice thing about these expressions is that it is possible to create them separately and add them together later and get a relatively normal Maxima expression. (There are some hiccups if you try to differentiate or integrate them.) I can't comment on the performance of the characteristic function approach versus the if-then-else approach, but the characteristic function approach may be more manageable to produce.

The Program
There are a number of details that don't specifically relate to this problem that I will not go into detail about and other details I have given in the two previously mentioned posts on bulge factors. Here is the complete code for producing the parametric equations and plotting them followed by the result for a specific example polyline.

:lisp (defun |$MINLENGTHP| (maxima-list min-length)   (loop for p in maxima-list      for i = 1 then (1+ i)        if (> i min-length) return t))

load(interpol)$ maperror: false$ mapprint: false$ ratprint: false$ justpoint(u) := [u[1],u[2]]$ turn_right(direction) := [direction[2], -direction[1]]$ rotation_sign(dirA, dirB) := -signum(justpoint(dirA) . turn_right(dirB))$ deflection_sign(a,b,c) := rotation_sign(b-a,c-b)$ magnitude(v) := sqrt(v . v)$ polyseglength(a,b) := block([run,radius,bulge,centralAngle], run: magnitude(justpoint(b-a)), bulge: a[3], if bulge = 0 then run else ( radius: run/4*(1/bulge + bulge), centralAngle: atan(bulge)*4, centralAngle*radius))$ /* negative bulge does not cause an issue for this calc; comes out in the wash */ /* returns [center,radius,rise,run,altitude,bulge_normal] */ arc_everything(a,b) := block([dir,u,norm,bulge,s,rise,radius,alt], dir: justpoint(b-a), u: magnitude(dir), norm: turn_right(dir)/u, bulge: a[3], s: signum(bulge), rise: abs(bulge)*u/2, radius: u/4*(1/abs(bulge) + abs(bulge)), alt: radius - rise, [(a+b)/2 - s*alt*norm,radius,rise,u,alt,norm])$ parametric_line(A,B,start,parameter) := justpoint(A) + justpoint(B-A)/magnitude(justpoint(B-A)) * (parameter - start)$ parametric_arc(A,B,start,parameter) := block([center,radius,rise,run,altitude,bulge_normal,sig,theta_i,theta], [center,radius,rise,run,altitude,bulge_normal]: arc_everything(A,B), sig: signum(A[3]), [x,y]: (justpoint(A)-center)/magnitude(justpoint(A)-center), theta_i: atan2(y,x), theta: theta_i + sig * (parameter - start)/radius, center + radius*[cos(theta),sin(theta)])$ parametric_polyline(polyline,parameter) := block([cumlen,cumlen2,current,poly], cumlen: 0.0, current: polyline, poly: 0, while minlengthp(current,2) do ( term: if current[1][3] = 0 then parametric_line(current[1],current[2],cumlen,parameter) else parametric_arc(current[1],current[2],cumlen,parameter), cumlen2: cumlen + polyseglength(current[1],current[2]), poly: poly + charfun2(parameter,cumlen,cumlen2)*term, cumlen: cumlen2, current: rest(current)), [parametric,poly[1],poly[2],[parameter,0.0,cumlen-10^-8]])$ pl: [[0,0,0],[0.2805351111430803,0.2805351111430803,-0.1989123673796571], [0.4568168316928867,0.3535533905932737,0],[2.854253390593276,0.3535533905932737,-0.4142135623731028], [3.103553390593274,0.1042533905932738,0],[3.103553390593274,-3.0,-1.0],[0.0,-3.0,0.5], [1.5,-2.0,0]]$ p: parametric_polyline(pl,t)$ plot2d([p],[same_xy,true])$

Defining a User Coordinate System

In AutoCAD you have User Coordinate Systems (UCS) and the World Coordinate System (WCS). The WCS is the system which your model information is stored in. The UCS is what you draw in. When you first begin a drawing, the current UCS is the same as the WCS.

First, let's familiarize ourselves with how the WCS looks. I've drawn a pyramid in AutoCAD and shown it from several different angles:

The WCS is displayed in all four pictures (and, naturally, is exactly the same in each picture).  One of the techniques for dealing with 3D when you are "doing the math" (perhaps in your own code) and want to make sure the math (or code) you're writing matches the geometry you're working with is known as "the right hand rule."  (We're going to use this for some math coming up in a few paragraphs.) For each picture, look at the WCS and orient your right hand (which should be open face initially) so that your fingers are pointing in the direction of the x-axis and your palm is open toward the direction of the y-axis.  (Don't think about your arm, just your hand. The arm will just go wherever it needs to go, though it may look funny to onlookers.)  Curl your fingers into your palm and stick your thumb out. If you've done it correctly, your thumb should be pointing in the direction of the z-axis.  If you can do this with all four pictures, you're well on your way to being able to understand the rest of the math in this post.

In math notation, we might write the relationship above as something like z = x × y.  The relationships which apply to the WCS (and all UCSs) are

• x = y × z
• y = z × x
• z = x × y

Two of the best ways to change the UCS in AutoCAD are

• Rotate around a chosen axis:  this is one of the more intuitive ways to adjust the current UCS when you don't have "pickable points" in the plane you want the new xy-plane to be in.
• Pick three points:  this is a way to put the current UCS in line with a face or in line with somewhere you want to put a face.  Lining up with an existing face of a 3D drawing only requires to you to pick three of the corners of the face.  Depending on the order you pick those points in, you will get different directions for the axes, but the xy-plane of the new UCS will coincide with the three points you pick.

So, how do you define a UCS based on a three points?  Three points define a plane, but that isn't enough to define a UCS.  You need to know where the origin is, which direction the new x-axis is to go, which way the new y-axis is to go, and you also need to pick a direction for the z-axis that is consistent with the way the z-axis relates to the xy-plane in the WCS.  Note that if we just solved the equation of a plane (Ax + By + Cz + D = 0) for the three points we start with, we would not know which way the z-axis goes.  Is it above the plane? below? and why?

To obtain consistent definitions for these axes we use the cross product (which I tried to sneak in earlier:  z = x × y).  Here's the definition of the cross product:

        a × b = (a₂ b₃ - b₂ a₃, a₃ b₁ - b₃ a₁, a₁ b₂ - a₂ b₁),

where a = (a₁, a₂, a₃) and b = (b₁, b₂, b₃). Think about these vectors as direction vectors as opposed to points.  One of the important properties of the cross product is that it produces a vector which is perpendicular to both of the vectors that form the product. That is, a × b is perpendicular to a and to b. To determine which way a × b is pointing, point your fingers (using your right hand) in the direction of a with your palm facing in a direction such that you can curl your fingers toward b.  Your thumb is pointing in the direction of a × b.

Here's how a UCS is defined based on three points. The first point (P₀) indicates the position of the new origin. The second point (P₁) defines the direction from the first point the x-axis goes in. So, the direction of the new x-axis is x = P₁ − P₀. The third point (P₂) determines not only the plane, but also which side of the x-axis the y-axis will go (within the defined plane). At the same time, we are also defining, albeit indirectly, the direction of the z-axis by means of the right hand rule. We define our UCS accordingly:

• Origin: P₀
• x-axis: x = P₁ − P₀
• z-axis: z = x × (P₂ − P₀)
• y-axis: y = z × x

Notice the z-axis is defined before the y-axis as well as the order of factors which produce y. Also observe that the order in which you select the points affects which way your axes are oriented, even though it will not affect what plane is the xy-plane of your new UCS. Given any three points, there are three possible origins - so I need to specify which is the origin. With that selected, I have two options for which will indicate the direction of my x-axis. So, there are six possible UCSs given the same three points in different orders.

Depending on the use of your UCS (if you are programming one in your own software) you may wish to normalize the direction vectors. Normalized vectors (which have length equal to unity) have some useful properties which may save some computation in later calculations. Normalizing is straightforward and simply requires you to divide the value of each component of the vector by the current length of the vector.

The Polygon Worksheet

I have put together a worksheet in Excel to demonstrate a technique for calculating the vertices of a regular polygon.  You can download the worksheet here.

Overview

It demonstrates an application of vector rotation (and, by the way, complex number multiplication makes a good way to remember how to do vector rotation).  The motivating principle is to demonstrate how you can reduce calls to trigonometric functions while calculating vertices of a regular polygon.  Note that the spreadsheet does not give such (time) savings because it uses both methods: (1) direct calls to trig functions for each vertex in columns B and C and (2) vector rotation in columns E and F.  Also, the error of the vector rotation results is given in columns H and I.  You will notice that the error becomes larger as the vertex number increases.  The error occurs in the vector rotation method, not the trig function method (which is our control, since we believe these results represent the best approximation we can achieve using the floating point precision available in Excel).

The only values you should need to adjust are the number of sides cell, the radius cell, and the initial angle cell.  Everything else follows from these values.  A few notes are in order:

1. The polygon that is determined, is inscribed inside of the circle with the given radius, and centered around the origin. 
2. All angles are specified and calculated in radian measure.
3. If fewer than 50 vertices are needed, the rows will repeat.
4. If you wanted the center somewhere other than the origin, just apply a translation to the points.  So, if you want center (a, b), then each point P = (x, y), becomes P' = (x + a, y + b).  If you've made it this far into this post, you are probably more than capable.

Why Try to Reduce Calls to Trig Functions?

As the user of calculation software and scientific calculators, you may be wondering why we would want to reduce our use of trig functions.  The main reason would be for time-critical applications.  This particular spreadsheet is obviously not one of those, but it demonstrates the accuracy of the method.  So, how do I know that trigonometric functions take a long time to perform.  First of all, let me debunk some myths:

1. Computers and calculators have tables of numbers in them that they use to determine values of "complicated" functions.  So wrong!  Computers and calculators compute/calculate these values!
2. The calculations that computers and calculators do are just based on tables and interpolation.  This is rarely true.  Sometimes a programmer will use a method like this when he knows that the precision needs of his application will be met this way and will be much faster.  But it is actually more programming effort and would only be done when you didn't need very accurate results but you needed them really, really fast.
3. Computers and calculators have hardware circuits that make the complex calculations almost as fast as the simple ones.  Not so.  Fact:  Multiplication is done with the fmult instruction.  Addition is done with the fadd instruction.  fmult takes way, way more computer cycles to compute than fadd.  fsincos takes way, way longer than fmult.  It is an unavoidable consequence of the nature of these calculations.

Recall that multiplication is dependant on addition.  Several additions actually.  So it should come as no surprise that by the time you put together a circuit that does the job that several additions and small multiplications can do, you end up with a circuit that takes longer to complete than one that just does addition.

The same is true of trig functions.  You know how you calculate them?  Here are the magic formulas:

The dots (...) indicate that it goes on and on and on and on and on, until the changes are small enough that you aren't changing the digits that mater to you. You may need more terms than are listed to get the accuracy you need. These formulas above are not written in the most computationally efficient manner, but you can rest assured that any circuitry or coding or combination thereof, which computes the values of the above functions will take longer than 4 multiplications and 2 addition/subtractions will (those are the operations involved in doing vector rotation).

Enter Vector Rotation

The key to how this method helps us, is that we can use a few trig function calls at the beginning and reuse the results several times over. We compute the direction vector for the central angle, θ, that each side covers. For a hexagon, this angle is 360°/6 = 60°, or π/3.

We need to determine the value of the central angle using direct calls to trig functions, but we will be able to reuse those values.  We also call trig functions to get our initial position.  From there we use our vector rotation method.  So, E14 and F14 use the values in E11 and F11 (renamed mx and my) and those of E13 and F13 to find their values:

E14 =E13*mx-F13*my

F14 =E13*my+F13*mx

Cells in rows below 14 do the same thing.  They still reference mx and my, which are the cosine and sine of our central angle, θ, respectively, and they reference the cells directly above them.  The concept for each row is:  rotate the point in the row above me around the origin by the central angle and tell me the x and y values for that rotated point.

Proof of the Formulas

Suppose we are given a point (x, y) and denote the distance from the origin as r and the angle it makes with the positive axis as i.  We wish to rotate (x, y) counter-clockwise about the origin by angle θ.  The diagram below illustrates:

Our new point (x', y') can be simplified:

                  

                      
                      
                 
                     
                     

If you look back at the formulas for E14 and F14, you may observe that mx and my correspond with sin θ and cos θ and E13 and F13 correspond with x and y.  That's all there is to it. 

Relationship with Complex Number Multiplication

If we represent the new point (x', y') as x' + y'j (where j is used to indicate the square root of -1), we can say:

This will produce an equivalent result to what we have above.