Bulge Value (code 42) in LWPolyline

Polylines are a pretty handy way to represent and manipulate outlines of objects in CAD software. However, the very robust polyline entity can do so many things that it is somewhat complicated. The light weight polyline (LWPolyline) entity is a trimmed down version of polylines that does the most frequently needed things fairly compactly and straight-fowardly.

LWPolylines are strictly 2D objects. Of course, they can be created in a UCS other than the WCS but they will be planar, and the points stored in them will be 2D points relative to their object coordinate system (OCS—I haven't really worked with OCSs so I'm not much help other than to tell you to learn the Arbitrary Axis Algorithm described in the free DXF Reference from Autodesk, which I've never actually learned properly).

LWPolylines still have the ability to represent arcs. Actually, I don't know how these are represented in Polylines, but in LWPolylines, arcs are fairly simple. All you need is the bulge value (code 42) which is tan(θ/4), where θ is the central angle.

Fig.1. θ is the central angle.

Which raises an interesting question: why for do we need the tangent of a quarter of the central angle?

Fig. 2. If the arc above was drawn from A to B, the bulge value would be negative (CW).

One reason is that it is compact. Other than storing points A and B, which you already need, the only additional information to unambiguously denote the arc from A to B is the bulge value. If the radius was stored instead, we would have up to 4 different arcs that could be being referred to. The SVG representation requires you to enter two parameters after the radius that clarify which of the four arcs you want. SVG is trying to be human reader friendly, but in DXF, we're not as worried about that. I find it easier to deal with the bulge as far as computations are concerned.

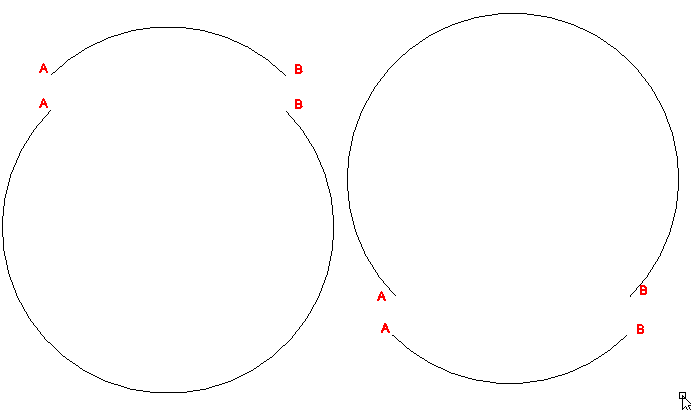Fig. 3. Four possible arcs of a given radius drawn from A to B. Which one do you want?

I imagine the choice of storing the tangent of the angle is computation speed. The choice of a quarter of the angle is probably for two reasons:

1. Tangent has a period of 180°. Now, if you used the tangent of half the angle subtended, this might appear initially to be sufficient, except that you would not be able to use the sign of the value to decide between CW and CCW since you would need the sign to decide between less than or greater than 180° arcs. You would also have an asymptote get in the way of drawing semi-circles. By storing the tangent of a quarter of the arc subtended, we restrict the the domain to angles which yield a positive tangent and so the sign value can be used for something else. It also avoids data representation limitations until you get close to having a complete circle (at which point, the user should probably consider using a circle). I don't know what the solution technically would be for storing a full circle other than a key value or just not letting the user do that—don't know what happens.
2. The diagram above shows some handy interrelationships that allow us to fairly easily calculate the rise (i), the radius, the peak (P), and the center (C). A bit of algebra produces \(r = \frac{u (b^2+1)}{4b}\) and \(i = \frac{b u}{2}\), where \(b\) is the bulge value and \(u\), \(r\) and \(i\) are as in Fig. 2. Calculating \(u\) unfortunately requires a square root, but no trigonometric function calls. Finding C and P involves using \(r\) and \(i\) along with a vector perpendicular to line AB [e.g., \((x,y) \to (-y,x) \), but watch which one gets the negative depending on which way you're turning].

(See Polylines: Radius-Bulge Turnaround for follow up post to this one.)