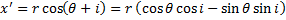Degree of Saturation versus Relative Humidity

These two quantities are similar and as I worked through ASHRAE Handbook Fundamentals (2009) IP, chapter 1, I was initially baffled as to what the difference was.  First, the definitions based on ASHRAE Fundamentals:

Relative humidity:  The mole fraction of water vapour in a sample divided by the mole fraction of water vapour in saturated air at the same temperature and pressure.

Degree of saturation:  The humidity ratio of water vapour in a sample divided by the humidity ratio of water vapour in saturated air at the same temperature and pressure.

Humidity ratio:  The humidity ratio is the mass of water vapour divided by the mass of dry air in a sample. This value can also be expressed in terms of molar fractions.

Discussion of Differences

In relative humidity, imagine taking two samples, one of the air which you want to know the relative humidity of and one of saturated air at the same temperature and pressure. For example, we might take samples of 1 mole each. In the non-saturated air, we will have less water vapour than in the saturated air. On the other hand, we will have more dry air in the non-saturated sample than in the saturated sample. The same general relationship will be true of mass, but the masses and the mole fractions will relate differently due to differing molecular masses. Here's the bottom line: we compare the samples based on moles (which amounts to the number of molecules) not on a given mass or volume. When you're dealing with gases, moles is the way to go.  In other words, our non-saturated and saturated samples relate by the equation:

where the items on the left hand side are the mole fractions of water vapour and dry air in the non-saturated sample and the items on the right hand side are for saturated air.

Understanding that we need to compare these quantities with a fixed number of total moles as in the previous equation is what makes ASHRAE's equation (14) work out.  From the last given equation we have

Therefore,

which verifies equation (14) as given in ASHRAE Fundamentals (2009).

It is worth noting that we only had to worry about this molar equality in developing this equation. When it comes to computing the degree of saturation from the relative humidity and vice versa, we don't have to think about that. The formula will do that for us. Also, we can still compute the degree of saturation directly from values off of a psychrometric chart (for example) by reading across to the right to get \(W\)and finding \(W_S\) by finding where the dry bulb temperature intersects the saturation curve and reading across to the right.  The definition of degree of saturation doesn't require us to account for the number of moles, only the relative humidity (and yes, if you're using charts you can read it off there as well).  If you are familiar with reading psychrometric charts, you will know that reading W values is generally much easier than reading RH values.

So if you're getting different values for these quantities in your work, it's not (necessarily) a mistake or a misreading of the chart—they really are different.

Convective Heat Transfer on a Building Envelope (Wind Chill?)

I'd like to make a brief mathematical investigation into the concept of a wind chill factor and how one particular scheme common in popular culture (and even affecting some in industry) does not relate well to modelling of a building envelope.  Wind chill is the temperature which a human being perceives accounting for the effects of wind and temperature together.  The preceding sentence is awkward because it is trying to say too much at once, so let me try again:

A wind chill index (expressed in units equivalent(ish) to temperature measurements) is answering a question:  What temperature T_WC (with wind speed = 0) will be perceived by a human being as equivalent to temperature T_actual (with wind speed = V_actual)?  (We are talking here more particularly about the exposed skin of a human being.  Also, it isn't purely a matter of perception.)

Human beings, not buildings.  Consider the following differences:

• buildings (in cold climates) have a much lower surface temperature than humans
• the amount (and temperature) of moisture on their surfaces is generally different and has a different internal transport mechanism (brick has basically no moisture and that moisture is already cold, human skin normally has moisture—perspiration—which evaporates more rapidly in windy conditions than calm conditions causing heat loss, because evaporation requires energy)
• unlike human beings, buildings do not have psychological comfort issues affecting their perception of temperature (and, admittedly, cannot reasonably be considered to perceive anything)

The equation used today for wind chill index has some theoretical basis but in the end is empirically derived.  That means they did experiments and found something that "works".  It is a very pragmatic way to deal with complex issues, especially ones that include psychological/cognitive components.  (I'm not "disrespecting" empirical equations, they're useful.)

So, where do I start? I would hard pressed with my current knowledge/understanding to deal with the evaporative cooling effects on human skin as compared with buildings, though such investigation might be meritorious. I will not attempt to compare the psychology of buildings with that of humans—I hope you understand. I will however seek to show how the concept of an "equivalent temperature in the absence of wind" yields different results depending on the surface temperature of the material in question. As such, although we will not compare human skin with face brick, we will compare warm Surface X with cool Surface X.

Convective Heat Transfer

The convective heat transfer equation is simple enough:

                q = h_c A_S (T_S – T_air)

where q is the heat energy (per unit time), h_c is the heat transfer coefficient, A_S is the surface area, T_S is the temperature of the surface and T_air is the ambient air temperature.
The heat transfer coefficient varies with wind speed.  Suppose we want to find an air temperature T_WC (no wind, h_NW) which causes the same rate of heat loss as T_actual (wind speed = W_actual, h_actual).  In that case, we need to relate:

                h_NW A_S (T_S – T_WC) = q = h_actual A_S (T_S – T_actual),

which simplifies to

               T_WC = T_S – (h_actual / h_NW)(T_S – T_actual).

A Little Problem

This leaves me with a problem. I want to have some type of reasonable value for the convective heat transfer coefficient ratio (h_actual / h_NW).  How do I get that?  I will engage in a little pragmatism and pretend that the wind chill equation will still give me a way to get an (h_actual / h_NW) ratio. This is perhaps a dubious step, but may suffice for illustrative purposes. From the wind chill equation we get a 15 mph wind at -31°F being equivalent to no wind at -59°F. Here's what we get for the ratio for human skin (which I have to use since that's what the wind chill equation is based on):

            (h_actual / h_NW) =  (T_S – T_WC) / (T_S – T_actual)
                                   =  (88 – (-59)) / (88 – (-31))
                                   = 1.235

(I've used 88°F for human skin, but that temperature will be different depending on the ambient temperature. Oh, well, what do you do when you live in a shoe?)

Theoretically, the convective heat transfer coefficient is largely independent of temperature and area, but it will change based on the interaction of the fluid and the surface which will include things like geometry, orientation, surface roughness, moisture, etc.  Unfortunately, temperature differences may affect the actual coefficient. They will affect the result if you consider radiation losses as well, since radiation transport is proportional to absolute temperature to the fourth power.

Wind Chill Effect on Surfaces at Different Temperatures Than Human Skin?

So, let's consider a surface which is maintained at a temperature of 10°F and is surrounded by an ambient temperature of -31°F and the wind speed is 15 mph.  (This is not the temperature in the boundary layer. The point of the convective heat transfer equation is to deal with this phenomenon in a simplified way—essentially to circumvent it.)  So, what's my "equivalent temperature in the absence of wind"?

               T_WC = T_S – (h_actual / h_NW)(T_S – T_actual)
                       = 10 – 1.235 (10 – (-31))
                       = -40.6 °F

So, the rate of heat loss from Surface X under the actual conditions is the same as the rate of heat loss for Surface X with no wind and a temperature of -40.6°F.

We obtained a different value than we did for the wind chill index applicable to human skin. The reason is straightforward: the rate of heat loss is proportional to the difference between the ambient air temperature and the surface temperature. Now, if it is -31°F outside, what temperature is the outside surface of a building? Perhaps -21°F? This makes quite a difference:

               T_WC = T_S – (h_actual / h_NW)(T_S – T_actual)
                       = -21 – 1.235 (-21 – (-31))
                       = -33.4 °F

So the effect is not zero, but it isn't much to talk about. If my h ratio is actually much higher, we will get a greater difference.

Considerations on Building Outside Surface Temperatures

The thickness and properties of the building envelope materials may change the relationship between ambient air temperature and surface temperature. Such changes will change the rate of heat loss in proportion to the temperature difference. Is there a higher difference at glazing surfaces than concrete surfaces?

There's also a sticky point regarding solar heat gains. Such gains on the surface will increase the rate of heat loss at the surface. But watch out! This is mainly behaviour occurring at the surface. We're dealing with a cold climate situation. Radiant heat from the sun heats up the surface only to be removed by increased rates of convection and radiation loss. This does not help us analyze the heat losses from the interior of the building! Plain "horse sense" tells me that adding thermal energy to the exterior does not cause a net increase to the rate of heat loss from the building interior. At worst, the increased rate of convective (and radiation) loss will remove all of the radiant energy added. To deal thoroughly with this issue, we would either need to model both together (allowing them to interact numerically with each other—for transient analysis) or use a "net direct solar gain" approach that deals with the interaction of convection and radiation (gains and losses) at the surface in an integrated way. The obvious outcome is that the rate of heat loss from the interior is reduced, but determining how much could be fun times.

Note that in warm climate conditions (cooling conditions), heat on the outside surface migrates toward the interior and we must therefore consider it. It is no longer starting to go in only to double back* (as it were), but actually conducting through the envelope and so directly affecting interior conditions. (*Analogical language enjoys talking about physics.)

CAUTION: This is NOT a Final Answer

In closing, this article is not trying to present the final answer to this problem. Rather I am attempting to expose the fallacy that the wind chill index (and corresponding formula) can be naively applied to energy modelling problems in building science. Furthermore, my criticism is not directed against nor does it address considerations of the effects of wind on air leakage analysis.

Note that ASHRAE Fundamentals chapter 26 (2009) gives effective R-values which can be used. The point of these values is to bypass all of the stuff I'm writing about in this article and account for convection and radiation losses at the surface under a 15 mph wind design condition. You don't actually need all that wind chill stuff—chapter 26 R-values already give a reasonable estimate of the wind effects, i.e., R-0.17 at 15 mph on the exterior instead of R-0.68 on the interior for still air at a wall.

Linear Interpolation Made Convenient in Maxima

load(interpol); pts: [[0,5],[1,1.5],[4.4,3.14159],[10,10]]; f(x) := ''(linearinterpol(pts,varname='x)); g(x) := ''(cspline(pts,varname='x)); wxplot2d([f(t)],[t,-5,15]); wxplot2d([g(t)],[t,-5,15]); wxplot2d([f(t)],[t,0,10]); wxplot2d([g(t)],[t,0,10]);

(I usually put the load statement in a separate cell in wxMaxima so that I am not re-executing the load every time I correct my main code and rerun the cell.  Minor point.)

Maxima can turn a set of points into a function for linear interpolation.  For that matter, it can make a cubic spline out of the same points.  I'm more interested in the linear interpolated function today—the other is for your reference.  There are three main points of interest in the above code:

1. linearinterpol() takes points, sorts them by the first ordinate, and produces an expression.
2. linearinterpol() produces expressions which use the characteristic function, rather than taking cases to make it transparent to other Maxima routines.
3. The use of the double single quote operator ('') and the single quote operator (') helps me to define the function f(x) such that x is a formal variable and not embedded as an expression.
4. linearinterpol() produces an expression which extrapolates beyond the specified points (from negative infinity to positive infinity) and it is left to the user's discretion to determine the limits to which this extrapolation is reasonable or applicable.

In a Nutshell

All you need is a list of 2D points.  There is more than one way to specify these, but I find it easiest to use a list of lists.  The main list elements are all lists of 2 representing x and y ordinates.  The function sorts these points according to the x-coordinate before proceeding.  You can specify the variable which will be used in the expression.  Provided that you precede that variable with a single quote operator, you can use a variable that is elsewhere assigned a value.  More on that below.

Transparent Output

The characteristic function, which is often assigned the Greek letter chi ("χ"), returns either 0 or 1.  It is a function of two variables, a set and a value.  If the value is an element of the set, it returns 1, otherwise it returns 0.  In the context of our linear interpolation expression, we have a linear expression for each interval in our set of points and each of these is multiplied by a characteristic function with a different set.  Since the sets used for the characteristic functions form a partition of the real numbers, we won't have more than one of the terms of our overall expression from linearinterpol() evaluate to a non-zero value at a time.  This expression can be integrated, differentiated, or combined with other expressions without having to take special cases.  Take the monkey off your back, let Maxima do it.

Cool, Useful, but Initially Abstruse Operators

The single quote operator (beside the key) is a way to tell Maxima, "Don't evaluate this thing."  If I write x and x is assigned value, then Maxima will do what is normally very helpful to me, namely, make the substitution for me.  If I don't want Maxima to do that, because I actually want the expression x, not the value that x stands for (because it has been assigned a value), I need to write 'x instead. In contrast, the double single quote operator ('') tells Maxima to replace the given expression with the value of the expression. This way, when I use the delayed assignment operator (:=) it does not delay the execution of the linearinterpol() function, only the evaluation of the expression as a function of x is delayed.  You may recall from my previous post that parameters in function declarations are formal.  Even if x is elsewhere assigned a value, f(x) := some_expression_including_x + x, will still work intuitively.

Here is some sample input followed by the output.  This is the best way to clarify in your mind the use of these operators:

x:2;
y:2*x;
z: 2*'x;
d(x) := z;
d(2);
d(3);
h(x) := ''(z);
h(2);
h(3);

(%o46) 2
(%o47) 4
(%o48) 2*x
(%o49) d(x):=z
(%o50) 2*x
(%o51) 2*x
(%o52) h(x):=2*x
(%o53) 4
(%o54) 6

Extrapolation

The expression that linearinterpol() produces does not protect you from yourself.  If will produce a result from negative to positive infinity without telling you that you have gone beyond the boundaries of your initial data set.  Actually, this is as it should be, in my opinion.  The program gives you the freedom to ask all the what-ifs your little heart desires, but it is up to you to discern what is really true to life and applicable to the particular problem you are trying to solve—whether the extrapolation is truly justified by the data is rightly left as a matter for user judgement.

Making a Double Out of Parts in VB.NET

Recently I picked up on a piece of code I had started several months ago and didn't have time to finish.  I was a bit stumped actually, though I've got it pretty well beat into shape now (maybe more on that later).  I was making a VB.NET type Fraction using BigIntegers as the base type.  As such, the class would theoretically be able to represent any rational number.  But what if I wanted to convert that result to a double?  So, I started into the code necessary to do the job.  I began with the easy part, the cases where the numerator and denominator can both be converted to doubles.  In that case, .NET already knows how to do the needed conversions.  But if the numerator or denominator is too large to be converted to a double, the result of division (mathematically) may still be within the range of a double.  For example,

4.445 × 10⁴⁰⁰ / 4.222 × 10³⁹⁹ = 10.528185693983894

An important finishing piece to solving this programming problem is the following function:

Public Shared Function DoubleByParts(positive As Boolean, exponent As Integer, mantissa As Int64) As Double Dim res As Int64 = 0 If Not positive Then res = &H8000000000000000 Dim biasedExp As Int64 = (exponent + 1023) If biasedExp > &H7FF Then Throw New OverflowException("Exponent too large for conversion to type Double.") If biasedExp < 0 Then Throw New OverflowException("Exponent too small for conversion to type Double.") If (mantissa And &HFFF0000000000000) <> 0 Then Throw New OverflowException("Significand too large for conversion to type Double.") biasedExp <<= 52 res = res Or biasedExp res = res Or mantissa Return BitConverter.Int64BitsToDouble(res) End Function

First, for a good summary of the double format, see Double-precision floating-point format (Wikipedia).

Code Walkthrough

The double type has 64 bits as does the Int64 type.  We begin with initializing our result variable to 0.  Depending on whether the number is indicated as positive or not, we set the sign bit.  The sign bit (bit 63, the most significant bit) needs to be set (1) to indicate a negative number.  For simplicity of use, I wanted to let the caller work in terms of the exponent (base 2) rather than with a biased result.  The 1023 "excess" or bias is one of those values you don't want to have to remember.  This function obviates the need to be overly conscious of that value.

After making our biased exponent (biasedExp), we check that it is in range.  We have exactly 11 bits to work with.  If our result is greater than 11 bits (0x7FF in hex, 11111111111 in binary), then we complain to the caller with an OverflowException.  If the result is negative, then it still does not fit into the 11 bits and we complain with an OverflowException in this case as well.  The mantissa is required to be no more than 52 bits.  That's 13 "nibbles" (4 bits, a single hex digit) or 6 1/2 bytes.  If the mantissa has any bits set in the upper 12 bits, we complain.  By calling the variable mantissa I have already declared my draconian intent with this function.  I will not coddle the caller by shifting things that are in the wrong place to the right place.  If the caller sends a mantissa which is too large, they may have done the shifting wrong or they may have incorrectly included the implicit 1 at the beginning of the "binary scientific notation."  Either way, the caller has made an error and we cannot know which one it is.  If we could know which error they made, it might make sense to correct it silently and move on.  However, a wrong assumption here could be somebody's program's undoing.  Therefore, we just complain and let the caller figure out what to do about it.

The biased exponent is now shifted into place—this, like the 1023 excess, falls into the category of "painful detail we want to encapsulate so we can forget about it."  (This is not ambiguous like the too-large-mantissa.)  In our final steps we "Or" the biased exponent and mantissa into place and use a call to BitConverter.Int64BitsToDouble() to ensure we have the proper format.

Room For Improvement

To make this function more robust, an exception class could be defined, either several different ones (one for each error) or a class with properties and enumerations to allow the caller to efficiently test for the particular condition that caused the "overflow".  I note also that I have used OverflowException where an underflow has occurred.  In program debugging, an accurate error message ("over" versus "under") can provide a clue to the person debugging the program.

How to make a .NET (Excel) Add-In Using Visual Basic Express 2010

Automation add-ins are easier than what follows and are the way to go if you just want a few custom functions.  Actually, for efficiency's sake, you might want to just use VBA functions added to Module1  (must be Module1—no renaming to a more suitable name) and then save the workbook as an Excel Add-In (*.xlam).  But, if it is user interaction or in some way making Excel "do stuff" (rather than just return a single result or an array of results), an add-in which implements the IDTExtensibility2 and IRibbonExtensibility interfaces may be a good strategy.  (The main alternative is to use VBA.)

Making an Excel Add-in in VB.NET involves the following (the ordering of the steps is not absolute):

1. Ensure you have Office installed on the development machine and have the Primary Interop Assemblies (PIAs) installed in the Global Assembly Cache (GAC).  You can download them from Microsoft.  (The Microsoft installer will put the PIAs in the GAC.)
2. Start a Class Library project in VB.NET.
3. It's a good idea to generate your own strong name using the sn.exe tool (part of the .NET framework).  You only need one for multiple projects.  In a nutshell, you use the sn.exe tool to create a *.snk file which you will tell VB.NET about.
• let VB.NET know where your *.snk file is by going to Project/Properties..., under Signing check "Sign the assembly" and choose a strong name key file.  You will be able to browse to where your *.snk file is
• if your add-in is intended to be widely distributed, and especially if you want to sell your add-in, you would be well-advised to learn more about this topic to ensure your end-users don't get warning messages that cause them to be (perhaps unduly) alarmed.
4. Apparently, step 4 is unnecessary, but I did step 4, so here it is:  In the project properties, go to Application and click the button Assembly Information....  In this screen, check the Make assembly COM-Visible box.
5. Create a GUID.  There are several ways but a program called guidgen.exe may already be on your computer which will do the job.  Just search your computer for it.  It is located under C:\Program Files\Microsoft SDKs\Windows\... on my computer.
• Copy and Paste the GUID into the Assembly Information... dialog box referred to in step 4.
6. Encapsulate your project in a namespace either by typing it explicitly in the files or by specifying a root namespace in the project properties.
7. Add references to needed PIAs, and extensibility (.NET tab)
• It is recommended that you add these by referencing the Interop Assembly on the .NET tab, not the COM tab. You may need to browse for this: Look under C:\Windows\assembly\gac_msil\Microsoft.Office.Interop.Excel\...
8. Create a class named Connect (seems that the name has to be Connect) which implements the IDTExtensibility2 and IRibbonExtensibility interfaces.
• Implements Extensibility.IDTExtensibility2, Microsoft.Office.Core.IRibbonExtensibility
9. Implement the methods of the interfaces.
10. Decorate the class with COM visibility specifications and include functions for creating and deleting custom registry settings.
11. Register your assembly with regasm.exe.

Steps 8, 9, and 10 are implemented in the following code snippet, which has been parameterized somewhat.

Imports System.Runtime.InteropServices Imports Extensibility Imports XL = Microsoft.Office.Interop.Excel <ClassInterface(ClassInterfaceType.AutoDual), ComVisible(True)> Public Class Connect Implements Extensibility.IDTExtensibility2, Microsoft.Office.Core.IRibbonExtensibility Dim oExcel As XL.Application Public Function GetCustomUI(RibbonID As String) As String Implements Microsoft.Office.Core.IRibbonExtensibility.GetCustomUI Dim res As String res = "<customui xmlns=""http://schemas.microsoft.com/office/2009/07/customui"">" res += "<ribbon>" res += "<qat/>" res += "<tabs>" res += "<tab id=""ArithmosTab"" label=""Arithmos"" insertBeforeQ=""TabFormat"">" res += "<group id=""exportGroup"" label=""Export"" autoScale=""true"">" res += "<button id=""secret111"" label=""Write Secret Number"" screentip=""See what the secret number is..."" imageMso=""DiagramTargetInsertClassic"" onAction=""WriteSecretNumber""/>" res += "</group>" res += "</tab>" res += "</tabs>" res += "</ribbon>" res += "</customUI>" Return res End Function Public Sub WriteSecretNumber(control As Microsoft.Office.Core.IRibbonControl) MsgBox("I don't know what you're talking about.") End Sub Public Sub OnStartupComplete(ByRef custom As System.Array) Implements IDTExtensibility2.OnStartupComplete End Sub Public Sub OnBeginShutdown(ByRef custom As System.Array) Implements IDTExtensibility2.OnBeginShutdown End Sub Public Sub OnDisconnection(RemoveMode As ext_DisconnectMode, ByRef custom As System.Array) Implements IDTExtensibility2.OnDisconnection End Sub Public Sub OnConnection(Application As Object, ConnectMode As ext_ConnectMode, AddInInst As Object, ByRef custom As System.Array) Implements IDTExtensibility2.OnConnection oExcel = Application End Sub Public Sub OnAddInsUpdate(ByRef custom As System.Array) Implements IDTExtensibility2.OnAddInsUpdate End Sub <ComRegisterFunctionAttribute()> Public Shared Sub RegisterFunction(ByVal pType As Type) Microsoft.Win32.Registry.ClassesRoot.CreateSubKey("CLSID\{" + pType.GUID.ToString.ToUpper() + "}\Programmable") Dim key As Microsoft.Win32.RegistryKey = Microsoft.Win32.Registry.ClassesRoot.OpenSubKey("CLSID\{" + pType.GUID.ToString.ToUpper() + "}\InprocServer32", True) key.SetValue("", System.Environment.SystemDirectory + "\mscoree.dll", Microsoft.Win32.RegistryValueKind.String) ' Add-in registry settings so Excel knows that this is an add-in and what it should do with it / register for all users key = Microsoft.Win32.Registry.LocalMachine.CreateSubKey("Software\Microsoft\Office\Excel\AddIns\<yournamespace>.Connect") key.SetValue("CommandLineSafe", 0, Microsoft.Win32.RegistryValueKind.DWord) key.SetValue("Description", "<description of your Add-in.>", Microsoft.Win32.RegistryValueKind.String) key.SetValue("LoadBehavior", 3, Microsoft.Win32.RegistryValueKind.DWord) ' if something goes wrong, tell the user what it is key.SetValue("FriendlyName", "<your friendly addin name>", Microsoft.Win32.RegistryValueKind.String) End Sub <ComUnregisterFunctionAttribute()> Public Shared Sub UnregisterFunction(ByVal pType As Type) Microsoft.Win32.Registry.ClassesRoot.DeleteSubKey("CLSID\{" + pType.GUID.ToString.ToUpper() + "}\Programmable", False) Microsoft.Win32.Registry.LocalMachine.DeleteSubKey("Software\Microsoft\Office\Excel\Addins\<yournamespace>.Connect", False) End Sub End Class

The functions RegisterFunction and UnregisterFunction are invoked by utilities like regasm.exe which comes with the .NET Framework.  I have created a batch file which I run in order to register the assembly.  You will need to modify it to suit your assembly.

cd C:\Users\<userid>\Documents\Visual Studio 2010\Projects\<projectname or names>\bin\Release C:\Windows\Microsoft.NET\Framework\v4.0.30319\regasm /codebase yourassembly.dll pause

Note that once the Add-in is registered and added, you will not need to reregister it after every Build (while developing).  

Get Your Text Data Into Maxima

Comma Separated Value (CSV) files are often a convenient way to move your text data between a variety of software products. The makeup of a CSV file is straightforward and can be observed by opening up a CSV file in a text editor. Excel provides the ability to save a worksheet to a CSV file.

Once your data is in a CSV file, you can read it into Maxima—with a little bit of code.

But, first, some house-keeping. In order to have convenient access to routines that you or someone else has written, you'll want to put the files that contain this code on Maxima's search path. The variables file_search_maxima and file_search_lisp, indicate the paths that Maxima will look through to find code to load. You can affect these values by modifying these during start-up (or any other run-time). Place a file called maxima-init.mac in the location indicated by the environment variable MAXIMA_USERDIR and place some code to the effect of the following in it:

file_search_maxima: 
    append(file_search_maxima, 
           ["fullpathto/Useful/Maxima/Functions/$$$.{mac,mc}"]);
file_search_lisp: 
    append(file_search_lisp, 
           ["fullpathto/Useful/Maxima/Functions/$$$.{o,lisp,lsp}"]);

(See here for more settings and see chapter 32. Runtime Environment.)

To see more about how to interoperate between Lisp and Maxima, see chapter 3 of the Maxima manual. The downloadable sample code shows how to use some of these techniques.

Download the following two files and place them in the directory you have added to your search path.

1. CSV.lisp
2. CSV.mac

Start up Maxima and then type and execute:

load(csv);

You will now have access to 4 functions to help you get your text data into Maxima.

---

Function:
CSVread(filename)

CSVread(filename,linesToSkip)

CSVread will read in the data in the file and turn it into a list of lists of string data. Each line of data becomes a separate list. Optionally, you may specify a positive integer value indicating how many rows to discard, which is handy if your data file contains (possibly multiple) header rows.

---

Function:
CSVNumberColumns(filename, skips, columnsToKeep)

CSVNumberColumns reads data in from the file specified by filename and skips skips rows of data (which may be 0). Additionally, it will excerpt the file by only retaining the columns requested in the list columnsToKeep. To keep all of the columns, pass in an empty list ([]). If you want the first and second column only, pass in [1,2]. All data in the columns which are to be retained is expected to be a valid Maxima expression in string form. Numeric or algebraic expressions qualify. Specifically, the data items must be something which the Maxima function parse_string can interpret.

---

Function:
MakeMatrix(d)

MakeMatrix creates a matrix with the data d, which is a list of lists. This is handy when you need your data in matrix form to pass along to a least squares function in Maxima, such as lsquares_estimates. Note that this function does not create a "deep" copy of the data in d. It is really just a separate "view" of the same data. As a note, I found that the display of the matrix results would sometimes be transposed. Only seemed to happen in output cells in Maxima and actual data format was as expected anyway (display glitch in my version of Maxima but not a consistent one).

---

Example:

load(csv)$ /* only needed once per Maxima start-up */
d: CSVNumberColumns("D:/path/circledata.csv",1,[2,3]);
m: MakeMatrix(d);

(%o9) [[1007.265919151515,1000.932075151515],[1008.902086,1002.038759],[1010.969034,1002.554592],[1013.1443,1002.268315],[1015.598881,1000.804232],[
1016.837804,998.9016388],[1017.35833,996.4303561],[1016.548809,993.5742165],[1014.687232,991.6508387],[1012.069706,990.6322456],[1009.539441,990.933599],[
1007.03337,992.4675972],[1005.545131,995.07334],[1005.520783,997.8698301]]
(%o10) matrix([1007.265919151515,1000.932075151515],[1008.902086,1002.038759],[1010.969034,1002.554592],[1013.1443,1002.268315],[1015.598881,1000.804232],[1016.837804,998.9016388],[1017.35833,996.4303561],[1016.548809,993.5742165],[1014.687232,991.6508387],[1012.069706,990.6322456],[1009.539441,990.933599],[1007.03337,992.4675972],[1005.545131,995.07334],[1005.520783,997.8698301])

Local Variables, Function Parameters, and Blocks In Maxima

One of the things that was a real hang-up for me when I started programming in Maxima was its seeming lack of variable scoping rules.  It made some irritating and non-intuitive things happen.  But, because I was always in “get-it-done” mode, I didn’t stop to figure out if there was a better way.  I would resort to adding letters to the name that I wanted to use.  If my functions were going to use a, I would instead name those aa, so that my variables in the “true” global realm wouldn’t be overwritten after the next function call.  My convention would then be, “nice names in the global realm, ugly names in the local realm.”  This is far from ideal.  The fact is, Maxima defaults to global variables, but makes it easy to declare local variables.

Maxima’s primary scoping mechanism is the “block.”  A block starts with block( and ends with ).  Each statement within a block is separated by a comma (,).  The first statement in your block should normally be [v_1, v_2,…,v_n], where v_1, v_2, etc., are variables that you wish to be local (don’t literally type v_1, etc.).  If you don’t want any local variables, then omit the local statement.

What Maxima actually does is not quite the same as in most programming languages, although the apparent runtime behaviour will be the same, if the [v_1, v_2,…,v_n] statement is used as above.  Maxima saves the current values of the variables in the [v_1, v_2,…,v_n] statement and essentially “zeros out” (removes their properties) those variables.  They become blank slates.  When Maxima exits the block() in which the variable was declared as local, its current properties are removed and the saved values/properties are restored.  As far as I know, Maxima does not support multi-threading.  This is probably a good thing, as temporarily preventing a variable from “existing” (as itself, that is; a variable with the same name is not the same variable itself, philosophically) is problematic if that variable could be accessed at any time by a separate thread.

This behaviour is different from most other programming languages which use “dynamic scoping” in that there are no save and restore steps of the kind we are talking about here (in most other languages).  In Maxima, variables have names at run-time and are referenced according to their name.  In most languages, the name of a variable is solely a convenience for programmers.  At run-time, values will move to various parts of the program memory space and the memory addresses will be determined on the fly (e.g., "placed on the stack").  Just because the same name is used in the source code for two variable references, doesn’t mean the compiled code will have references to the same memory location.  For example, t declared in function1() has nothing to do with t declared in function2().  These memory locations will be on the stack and exist only while each function is being executed.  This, again, is what is true in most programming languages, not in Maxima.

When it comes to function parameters, however, Maxima`s behaviour is not unlike most other languages.  That is, the parameters are formal.  They are not considered to constitute a variable declaration.  When I write

f(x) := x^2;

x is not declared as a variable.
Even if I write

RotationalEquivalenceSet(n, bits) := block(
    local(res, size),
    res: {n},
    size: 2^bits,
    if n >= size then return({}),
    n: 2*n,
    if n >= size then n: n - size + 1,
    do (
        if elementp(n, res) then return(res),
        res: union(res, {n}),
        n: 2 * n,
        if  n >= size then n: n - size + 1
    )   
);

n is not declared as a variable.  This is a very helpful thing.  If n was assigned some value before the function call, nothing that I do inside this function call (which uses n as the name of a parameter) affects that value.  The value of n will remain the same after this function has been invoked.  Here is an input/output example of the behaviour:

/* [wxMaxima: input   start ] */
n: x^2;
RotationalEquivalenceSet(3,5);
n;
RotationalEquivalenceSet(5,5);
n;
/* [wxMaxima: input   end   ] */
(%o21) x^2
(%o22) {3,6,12,17,24}
(%o23) x^2
(%o24) {5,9,10,18,20}
(%o25) x^2

Note that I am using := to declare these functions.  You may end up with different (and undesired) behaviour if you don’t use the “delayed evaluation” assignment statement.  If you want the usual programming paradigm with your function declaration, use := as per my sample code above.

DXFert: An Example VBA Add-In with Custom Ribbon

I implemented this project in Excel 2010. Only the Ribbon modifications are likely to be version dependent (unless you go way, way back). The form and macro in this project should work in any version of Excel.  

To use the macro launchmyForm(control as IRibbonControl)without the Ribbon buttons, such as you would need to do in an earlier version of Excel, you will need to either change

   launchmyForm(control As IRibbonControl) to launchmyForm() 

or 

write another macro that calls launchmyForm(someDummyObject).

In this post, I am going to walk through the building blocks of the project. Except for Excel, everything you need for this project is freely available for download.

What You Will Need to Develop Your Own Similar Project

1. Excel 2007 or later.
2. DXF file format documentation from AutoDesk
3. CustomUI Editor Tool from Open XML Developer
4. A program to allow you to test your DXF output (if that's what you're going for), such as DWG TrueView.

Overview

You need to 

1. create a UserForm within a macro-enabled workbook (*.xlsm)
2. write a one-liner macro that invokes the UserForm
3. create a Ribbon interface which references the one-liner macro, and, finally,
4. save the project as an Add-In (*.xlam) and activate it.

Creating the UserForm

If you don't have the developer tab available to you,...why ever not? Turn the silly thing on! To learn about developing user forms in Excel generally, there are lots of examples on the web, but I'll just give you a few key pieces of code that were important in my project.

Here's the code I used to open a file SaveAs dialog to help the user indicate the name and path for the file that the results will be exported:

Private Sub btn_Browse_Click() Dim fn fn = Application.GetSaveAsFilename(filefilter:="Drawing eXchange Format (*.dxf),*.dxf") If fn <> False Then Me.in_fileName.Text = fn End If End Sub

This should work in very early versions of Excel all the way up to the present (version 2010) and probably future versions as well.  My main beef with it is there is a lack of control.  I would like it to complain about the selection of a file which already exists, but if I really wanted to I could include that complaint in my macro code right before I follow through with the export (which I didn't do—but you can, if you wish).

When you want to terminate the form (either by cancelling or after successful completion), you'll want use something like this:

Private Sub btn_Cancel_Click() Unload Me End Sub

You can learn a lot about the DXF format by looking at my code in the download.  (Hint:  If you have the Add-In added, you don't need to open up the file separately to see the code.  Just go to the Visual Basic Editor (button on the developer tab) and locate the user form DXFout_Form.  Right-click it and choose View Code.)  See page 143 of the AutoDesk's DXF format documentation for a description of the fields in the polyline Entity.

The one-liner code which the Ribbon will call is pretty easy:

Sub launchMyForm(control As IRibbonControl) DXFout_Form.Show End Sub

The Ribbon expects to pass this control parameter to the subroutines it calls, whether you need to use the parameter or not.

Create the Ribbon Interface

I overcomplicated this my first few tries at it. Which is what a lot of people on the internet do. If you want your add-in to have its own ribbon elements, you create those elements using CustomUI Editor (referred to above) within a regular *.xlsm file. When you are ready to finalize it as an Add-In you just save it as an add-in and activate it. The same custom UI that showed up in the original *.xlsm file, will then show up all the time. No fuss, no muss. No Workbook_AddinInstall() code, no SetCustomUI(longComplicatedXMLString), no nothing, it just works! You do have to look at a bit of XML code, mind you.

But first, close down your *.xlsm file and open up CustomUI. Open up your *.xlsm file from within CustomUI. Go to the Insert menu and select Office 2010 Custom Part and, likewise, Office 2007 Custom Part. Now it is time for something ugly. Here is the xml code I used in my project:

For 2010 (customUI14):

<mso:customUI xmlns:mso="http://schemas.microsoft.com/office/2009/07/customui"> <mso:ribbon> <mso:qat/> <mso:tabs> <mso:tab id="dxfTab" label="DXF" insertBeforeQ="mso:TabFormat"> <mso:group id="exportGroup" label="Export" autoScale="true"> <mso:button id="highlightManualTasks" label="Export to DXF" imageMso="DiagramTargetInsertClassic" onAction="launchMyForm"/> </mso:group> </mso:tab> </mso:tabs> </mso:ribbon> </mso:customUI>

For 2007 (customUI):

<mso:customUI xmlns:mso="http://schemas.microsoft.com/office/2006/01/customui"> <mso:ribbon> <mso:qat/> <mso:tabs> <mso:tab id="dxfTab" label="DXF" insertBeforeQ="mso:TabFormat"> <mso:group id="exportGroup" label="Export"> <mso:button id="highlightManualTasks" label="Export to DXF" imageMso="DiagramTargetInsertClassic" onAction="launchMyForm"/> </mso:group> </mso:tab> </mso:tabs> </mso:ribbon> </mso:customUI>

If you look at the <mso:button> tag you'll notice the launchMyForm bit.  That's the name of the procedure that is to be called.  One parameter is passed, namely, the a reference to the ribbon control that called the subroutine.

Save As an Add-In

At any point, you can turn your *.xlsm project into an Add-In.  (You can even continue editing it while it is an Add-In.)  Go to File, Save As, and select Excel Add-In from the file type options in the SaveAs dialog box.

AutoDesk Design Review 2013 (0x2: Failed to download component.)

I said yes to updating my Design Review (2011) to the current version (2013) and got the above error message.  The solution in my case was to download the MSI file.  (Note:  click on the language you want under the Choose Your MSI column after instruction 2 at the linked location.)

After unzipping the .zip file you can just run the Setup.exe file.  The principle difference is that the downloading has already taken place and the setup program will look at your local or network location for the relevant files to install.

Now, to use Design Review 2013 without AutoCAD installed, you need to install TrueView.  If you have a version of AutoCAD installed on your computer which is temporarily without a current license (but it is installed on your computer), you'll need to explicitly tell Design Review to use TrueView.

To do so:

Within Design Review 2013, go to the main drop down menu (big "D" in top-left)
→ Options...(at the bottom middle right of drop down)
→ Click on the DWG Viewing tab
→ and check the box beside Open DWG files using DWG TrueView
→ Click OK.

Unfolded Approximation to a Hemisphere

The animated GIF featured below are a sort of slide show which give increasing levels of precision in polyhedral approximations to a hemisphere. The SVG one works properly in Google Chrome, but it may not work in all browsers. In theory, you could print these out, cut along the outline, and fold along the internal lines and you would have a polyhedral approximation to a sphere—if you use a lot of tape and your very best dexterity. More precisely, all of the corners would be coincident with the hemisphere being approximated. Notice that as the number of fold lines (latitudinal-ish lines) increases, for a given number of segments (longitudinal-ish divisions) the extent of the unfolded approximation approaches the grey line, which (probably) represents the limiting extent of these approximations. Specifically, this circle has radius of πr/2 or one fourth the circumference of the approximated sphere.

I wrote the code which generates this sequence of pictures in Maxima, a computer algebra system. The code is below and you can modify the range variable near the end to change the level of precision in the resulting pictures. The pattern for each range item is

[number of segments, [starting latitude divisions, ending latitude divisions]]

The "segments" are longitudinal segments like an orange. The latitude divisions are the number of latitude divisions in each of the segments.

load(draw)$ ExplodedHemiSphereLine(radius, deltaAlpha, theta) := block([line,vc,alpha,xpnm1,ypn,upperThresh,x,y,w,xpn], line: Polyline([0,0]), vc: radius*sqrt(2*(1-cos(deltaAlpha))), alpha: deltaAlpha, xpnm1: 0, ypn: 0, upperThresh: 3.14159265358979/2 + deltaAlpha/2, while alpha <= upperThresh do ( x: radius*sin(alpha), y: radius*cos(alpha), w: x*sqrt(2*(1-cos(theta))), xpn: w/2, dvn: sqrt(vc^2 - (xpn - xpnm1)^2), ypn: ypn + dvn, xpnm1: xpn, line: append(line, Polyline([xpn, ypn])), alpha: alpha + deltaAlpha ), return(line) )$ Reflect(points) := map(lambda([p],[-p[1],p[2]]), points)$ MakePrimaryLines(polyLine) := block([reflection,lis], reflection: Reflect(polyLine), lis: [polyLine, reflection], for i: 2 thru length(polyLine) do ( lis: append(lis, [Line(part(polyLine,i),part(reflection,i))]) ), return(lis) )$ RotatePoint(point, rotationVector) := [point[1]*rotationVector[1] - point[2]*rotationVector[2], point[1]*rotationVector[2] + point[2]*rotationVector[1]]; RotateLine(line, rotationVector) := block([p,res], res: part(line,0)(), for p in line do ( res: append(res, part(line, 0)(RotatePoint(p, rotationVector))) ), return(res) )$ RoundTheWorld(line, rotationVector, Ns) := block([lines,i], lines: [line], for i: 2 thru Ns do ( lines: append(lines, [RotateLine(lines[i-1], rotationVector)]) ), return(lines) )$ ExplodedHemiSphere(radius, Na, Ns) := block([deltaAlpha,theta,line,baseLines,allLines,rotationVector,obj], deltaAlpha: 3.14159265358979/(2*Na), theta: 2*3.14159265358979/Ns, line: ExplodedHemiSphereLine(radius, deltaAlpha, theta), baseLines: MakePrimaryLines(line), allLines: [], rotationVector: [cos(theta), sin(theta)], for obj in baseLines do ( allLines: append(allLines, RoundTheWorld(obj, rotationVector, Ns)) ), return(allLines) )$ FindMinMax(LineObjects, index) := block([min,max,p,obj], min: part(LineObjects[1],1)[index], max: min, for obj in LineObjects do ( for p in obj do ( if p[index] < min then ( min: p[index] ) else if p[index] > max then ( max: p[index] ) ) ), return([min, max]) )$ MakeScene(LineObjects) := block([res], res: gr2d(color = grey, fill_color = white, points_joined = true, point_type = none, axis_top = false, axis_bottom = false, axis_left = false, axis_right = false, xtics = none, ytics = none, ellipse(0,0,float(%pi/2),float(%pi/2),0,360), color = black), for obj in LineObjects do ( if part(obj, 0) = Line then ( res: append(res,gr2d(points([[part(obj,1)[1], part(obj,1)[2]], [part(obj,2)[1], part(obj,2)[2]]]))) ) else if part(obj, 0) = Polyline then ( res: append(res,gr2d(points(makelist([part(obj,i)[1],part(obj,i)[2]],i,1,length(obj))))) ) ), res )$ /* main */ ranges: [[3, [1, 3]], [4, [1, 4]],[5,[1,5]],[6,[1,6]],[7,[1,7]],[8,[1,8]],[9,[1,9]],[10,[1,10]],[11,[1,11]],[12,[1,12]],[13,[1,13]],[14,[1,14]],[15,[1,15]],[16,[1,16]],[17,[1,17]]]$ exp_ranges: map(lambda([u],makelist([1,i,u[1]],i,u[2][1],u[2][2])),ranges)$ ranges: []$ for i: 1 thru length(exp_ranges) do ranges: append(ranges,exp_ranges[i]); draw( delay = 100, dimensions = [500,500], file_name = "C:/Users/whateverpath/whatever", terminal = 'animated_gif, map(lambda([u],MakeScene(ExplodedHemiSphere(u[1],u[2],u[3]))),ranges) )$

Mathematics: Principles and Formulae

I gather that when most people think about mathematics, they think about two things, and in this order: numbers and formulas. In doing mathematics, most students are quick to add something else, though not by name: recipes – usually grossly oversimplified recipes. It is this tendency that runs them into so much trouble and many are the able teachers of mathematics that have tried to slap them (figuratively) into using something better, namely, principles.

A famous work of Sir Isaac Newton was titled, in Latin, Philosophiæ Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"). But you don't need to be as smart as Sir Isaac Newton to understand the importance of principles as superior to recipes. First of all, what's the difference?

A recipe is a sequence of steps or components with no (particular) reference to reasons. Computers do recipes - algorithms. Students that try to be computers (and nothing more) short-change themselves because there is already a much more efficient tool for that work than themselves. (And thus it is little wonder they complain about the pointlessness of the learning they are engaged in. Often of their own accord, they are not learning the really important lessons from mathematics that they should be.) Principles help me to justify, or at least partly understand, the steps of the recipe and apply it usefully. The ability Principles are one of the key advantages you have over your calculator.

People try to simplify the setting up and solving of proportion problems. They do it this way: "cross-multiply and divide." They don't really know why. It is only a recipe to them. How do you know which numbers to multiply and divide? It increases the number of things to memorize and (I have observed) it distracts people from the real principles. Forget about cross-multiplying and dividing. If I know a/b = c/d, I do what I always do with equations: do "opposites" and do the same thing to both sides (subject to the constraint that the operation must be permissible on the values in the equation). If I want to isolate a, I have a divided by b, so I do the opposite of divide by b, namely, I multiply by b, and I do it to both sides. The end. "Cross-multiple and divide" doesn't bridge well into solving other forms of equations, is unnecessary, gives little clue as to why it is supposed to work, and increases the number of things to memorize. How do you solve an equation?

1. Do "opposites."
2. Do the same thing to both sides.
3. Eliminate any apparent solutions which do not satisfy the original equations or the constraints of the problem (which may be implicit, such as, "negative area is not allowed").

Throw "cross-multiply and divide" and its ilk into the garbage bin.

Here are a few very generic principles to apply to problem solving:

1. Don't ask "What should I do?", ask "What is true?"  You won't make very much ground figuring out what to do if you haven't established a few things that you know about the situation. If you want something to do, then do this: find out more true things and organize them. This often starts with writing down some given information. Perhaps you print a few formulas and consider which variables you know and which you don't. Ask yourself, "Do I know any other equations that involve these unknowns? Are they valid in this situation?" Don't worry too much about whether an equation is going to give you the final answer, but concern yourself with whether it actually holds true in the situation. Thomas Edison didn't invent so many things by only trying things he knew would work. You also will write down formulas and find that they do not help you solve the problem – even though they are true and valid in the situation, they might not be useful to you. It isn't a mistake (yet), to write it down as a tool in the toolbox.
2. Don't ask "Why can't I do this?", ask, "Can this method or statement be proven correct?"  People want to apply rules that are applicable to one type of operation to a completely different operation. They see that they are allowed to make the statement a (b + c) = a b + a c and want to know why they can't say log(b + c) = log(b) + log(c).  This is one or both of two fundamental misunderstandings. Either it is assuming that the parentheses have the same meaning in both cases (which means they don't know what a function is and certainly not what a log is) or they misunderstand the importance of proof. This later misunderstanding in particularly important. Often the student assumes that a similar appearance means a similar treatment is permitted. The fact is, the statement a (b + c) = a b + a c, where a, b, and c are numbers can be proven. Our acceptance of the statement is based on proof from simpler principles. We don't "just know" that that's true (although this example is among the more intuitive that I could have chosen). Similarly, we don't "just know" that the statement  log(b + c) = log(b) + log(c) is true. If we can prove somehow that it is true, then we know we're allowed to make this expansion. On the other hand, if we can find a counter-example, we know it is not true. So here's a counter-example to the above (very, very silly) suggestion: log(10 + 10) = log 20 < 2, but log(10) + log(10) = 1 + 1 = 2; so they are clearly not equal. 
1. This doesn't mean you need to do proofs, but you should be satisfied that a proof exists for what you are doing and that you are not assuming something which cannot be established.
1. (Did you notice yourself proving your own work while you applied that principle? Tricky, huh?)
3. Look for patterns. Patterns have some kind of rule behind them. If you can determine the rule that makes the pattern, it may reduce work and memorization required. The rule will be more generic than the sampling that you noticed the pattern in – otherwise, it is a false pattern, because a counter-example exists. Don't assume the pattern is real. Test it, prove it, disprove it, as may be necessary.
4. Make analogies. The main reason for teaching the principle of proportional triangles is not to teach students how to solve triangle problems – although there's good uses for that. Proportions are so common place that everyone should get comfortable with the archetypical example: proportional triangles. There are analogies between force and momentum, between torque and force, momentum and rotational inertia, fluid pressure and electricity. Some things are more intuitive to us than others and if an analogy exists between something you are familiar with and something you are not, it can help you with a "working understanding" of the unfamiliar concept.

Understanding principles helps you to evaluate proposed solutions or solution methods. Recipes can't do that very effectively. Recipes also don't work well on a "new to you" problem. Knowing principles is a key point of difference between people who know how to implement a given method of solution and someone who can actually develop a method of solution to a problem they have not previously seen. This is true problem solving. Perhaps the most important thing anyone can do to improve their problem solving ability is to prize principles like gold and recipes as mere silver, maybe only bronze.

Angle Between Intersecting Planes

In a practical sense, there are a few different ways that you can go about determining the angle between two planes.  But before we get to specific methods and tools, let's try to lay the ground work – let's try to understand what we really mean by an angle between two planes.

Definition:  Angle Between Intersecting Planes

Two non-parallel planes intersect at a line.  The angle between intersecting planes is measured perpendicularly to this line of intersection.  In more detail, we can say, for planes P₁ and P₂ with line of intersection L:

1. The vertex of the angle between the planes is any given point on the line of intersection (that is, just pick one).
2. One arm of the angle is coincident with P₁ and the other arm is coincident with P_2.
3. Both arms of the angle are perpendicular to L.

Discussion of Definition

We note in passing that there is no need for the two arms of the angle to have any certain length nor is there a need for the lengths to be constrained by any relationship concerning relative lengths – they may differ.  Items 1 and 2 (above) should come as no surprise, but not everyone will immediately understand item 3.  Indeed, if you consider only the two trivial cases – (i) two coincident planes (technically excluded from discussion here) or (ii) perpendicular planes – item 3 appears superfluous.  To see that it is necessary, consider  planes which meet at a 45° angle (as an example).  Imagine putting a 45-45-90 triangle in place so that two of its edges are in contact with a plane each.  Suppose you made one of those planes rest on the top of the triangle and allowed that plane to rotate freely around the line of intersection (L).  Now, keeping the vertex of the triangle (the vertex on the line of intersection) in place and rotating the triangle around that point, you will find that the plane which is resting on the triangle will lift up – the angle between the planes will increase.  By the time you have rotated the triangle so that the vertical edge is against the "resting" plane, the angle between the planes will be 90°.
Here is a video where I demonstrate this scenario:


Perpendicular Angle Between Planes vs. Non-perpendicular Angle Between Planes
(Criteria 1, 2, and 3) vs. (Criteria 1 and 2)

In the above scenario we used the same triangle at different angles and changed the angle between the planes.  Now let's leave the planes be and change the triangle.  Let's draw the orthographic views of planes (represented as rectangles) intersecting at angle i, according to our criteria and draw two triangles in place:  one at 90° to the line of intersection and one at θ to the line of intersection.

I've been lazy in my drawing as the angle for β that I really want is in the plane of the triangle that's on an angle and not the angle of the orthographic projection of that triangle (which is what I have just drawn).  But bear with me.  The angle of intersection is given as i and we take the dimensions L and θ to be given.  From this information we can find formulae for R, h, and β.  Here are some formulae we can take directly off of the drawing:

\[\sin \theta = \frac{R}{L}\] \[\tan \beta = \frac{h}{L}\] \[\tan i = \frac{h}{R}\]

Manipulating these equations gives

\[R = L \sin \theta \] \[h = L \sin \theta \tan i \] \[\tan \beta = \sin \theta \tan i \]

Observe that β ≠ i.

Calculations Without a Scientific Calculator

You can obtain a rise and run for β without a scientific calculator by using a little measurement and geometry.  Suppose you are able to obtain a rise and run for each of angles i and θ.  You might do this by measuring either a shop drawing or a physical situation.  Choose the run arbitrarily and measure the rise which corresponds to it.  The hypotenuse (for θ) can either be measured or calculated using the Pythagorean theorem.  The formulae for the rise and run of β are simply

rise of β = (rise of θ) × (rise of i)

run of β = (hypotenuse of θ) × (run of i)

Defining a User Coordinate System

In AutoCAD you have User Coordinate Systems (UCS) and the World Coordinate System (WCS). The WCS is the system which your model information is stored in. The UCS is what you draw in. When you first begin a drawing, the current UCS is the same as the WCS.

First, let's familiarize ourselves with how the WCS looks. I've drawn a pyramid in AutoCAD and shown it from several different angles:

The WCS is displayed in all four pictures (and, naturally, is exactly the same in each picture).  One of the techniques for dealing with 3D when you are "doing the math" (perhaps in your own code) and want to make sure the math (or code) you're writing matches the geometry you're working with is known as "the right hand rule."  (We're going to use this for some math coming up in a few paragraphs.) For each picture, look at the WCS and orient your right hand (which should be open face initially) so that your fingers are pointing in the direction of the x-axis and your palm is open toward the direction of the y-axis.  (Don't think about your arm, just your hand. The arm will just go wherever it needs to go, though it may look funny to onlookers.)  Curl your fingers into your palm and stick your thumb out. If you've done it correctly, your thumb should be pointing in the direction of the z-axis.  If you can do this with all four pictures, you're well on your way to being able to understand the rest of the math in this post.

In math notation, we might write the relationship above as something like z = x × y.  The relationships which apply to the WCS (and all UCSs) are

• x = y × z
• y = z × x
• z = x × y

Two of the best ways to change the UCS in AutoCAD are

• Rotate around a chosen axis:  this is one of the more intuitive ways to adjust the current UCS when you don't have "pickable points" in the plane you want the new xy-plane to be in.
• Pick three points:  this is a way to put the current UCS in line with a face or in line with somewhere you want to put a face.  Lining up with an existing face of a 3D drawing only requires to you to pick three of the corners of the face.  Depending on the order you pick those points in, you will get different directions for the axes, but the xy-plane of the new UCS will coincide with the three points you pick.

So, how do you define a UCS based on a three points?  Three points define a plane, but that isn't enough to define a UCS.  You need to know where the origin is, which direction the new x-axis is to go, which way the new y-axis is to go, and you also need to pick a direction for the z-axis that is consistent with the way the z-axis relates to the xy-plane in the WCS.  Note that if we just solved the equation of a plane (Ax + By + Cz + D = 0) for the three points we start with, we would not know which way the z-axis goes.  Is it above the plane? below? and why?

To obtain consistent definitions for these axes we use the cross product (which I tried to sneak in earlier:  z = x × y).  Here's the definition of the cross product:

        a × b = (a₂ b₃ - b₂ a₃, a₃ b₁ - b₃ a₁, a₁ b₂ - a₂ b₁),

where a = (a₁, a₂, a₃) and b = (b₁, b₂, b₃). Think about these vectors as direction vectors as opposed to points.  One of the important properties of the cross product is that it produces a vector which is perpendicular to both of the vectors that form the product. That is, a × b is perpendicular to a and to b. To determine which way a × b is pointing, point your fingers (using your right hand) in the direction of a with your palm facing in a direction such that you can curl your fingers toward b.  Your thumb is pointing in the direction of a × b.

Here's how a UCS is defined based on three points. The first point (P₀) indicates the position of the new origin. The second point (P₁) defines the direction from the first point the x-axis goes in. So, the direction of the new x-axis is x = P₁ − P₀. The third point (P₂) determines not only the plane, but also which side of the x-axis the y-axis will go (within the defined plane). At the same time, we are also defining, albeit indirectly, the direction of the z-axis by means of the right hand rule. We define our UCS accordingly:

• Origin: P₀
• x-axis: x = P₁ − P₀
• z-axis: z = x × (P₂ − P₀)
• y-axis: y = z × x

Notice the z-axis is defined before the y-axis as well as the order of factors which produce y. Also observe that the order in which you select the points affects which way your axes are oriented, even though it will not affect what plane is the xy-plane of your new UCS. Given any three points, there are three possible origins - so I need to specify which is the origin. With that selected, I have two options for which will indicate the direction of my x-axis. So, there are six possible UCSs given the same three points in different orders.

Depending on the use of your UCS (if you are programming one in your own software) you may wish to normalize the direction vectors. Normalized vectors (which have length equal to unity) have some useful properties which may save some computation in later calculations. Normalizing is straightforward and simply requires you to divide the value of each component of the vector by the current length of the vector.

Best Fit Circle: find the center using Excel

Finding the center of a best fit circle depends on minimizing the same function we were concerned with in finding the radius, except that we are going to view it as a function of the center instead of as a function of the radius:

where a and b are the x- and y-coordinates, respectively, of the center and r is given by

What we have here is a function of two variables. It looks like three variables until you realize that r is calculated in terms of the other two. So, we can do a three dimensional plot and see what the scoop is. I used Maxima to do this and obtained a very good view of the surface near the best fit center of the points I have been using in all of my investigations of this problem. Here is the 3D plot of SSE(a,b):

What we are most encouraged to see in this graph is that it looks very smooth and it looks like there is exactly one point that is the lowest point. This lowest point is where the SSE function is minimized and constitutes the best center of the circle. (It might be that there are a few local minima somewhat close together that we could see if we zoomed up really tight to the bottom and we are probably happy with any of these as the "answer". Welcome to numerics.)

These formulae can be used in Excel. Designate two cells for each of the values a and b. You don't know what these are, but start with some guesses for these. You will reference these guesses in your Excel formulae. Put your points in consecutive rows after the pattern (x, y, se, R) where se references the x and y for that line as well as the values for a, b, and r. R will only reference x, y for that line and a, b from above. r above is the average of all the R values in the rows (don't include the 1/n in the R)--you may want to create a cell to contain this average and reference it in your se columns. Use absolute references for a, b, and r (if you have a cell for it) so you can copy and paste the formula easily. Make a sum formula at the bottom of your SSE column and it represents your SSE function as above. You want to use the Excel solver now. The SSE cell is the cell you tell it to minimize and the a and b cells you designate as the cells to be modified. The solver will tweak with the a and b values in an attempt to make SSE as small as possible. (The instructions about r and R might seem circular until you actually implement them. Follow through to the end and you'll see it really isn't circular.) Don't try too hard to follow the instructions--try to do the likely intent (as always).

For a Maxima approach see here.

The Polygon Worksheet

I have put together a worksheet in Excel to demonstrate a technique for calculating the vertices of a regular polygon.  You can download the worksheet here.

Overview

It demonstrates an application of vector rotation (and, by the way, complex number multiplication makes a good way to remember how to do vector rotation).  The motivating principle is to demonstrate how you can reduce calls to trigonometric functions while calculating vertices of a regular polygon.  Note that the spreadsheet does not give such (time) savings because it uses both methods: (1) direct calls to trig functions for each vertex in columns B and C and (2) vector rotation in columns E and F.  Also, the error of the vector rotation results is given in columns H and I.  You will notice that the error becomes larger as the vertex number increases.  The error occurs in the vector rotation method, not the trig function method (which is our control, since we believe these results represent the best approximation we can achieve using the floating point precision available in Excel).

The only values you should need to adjust are the number of sides cell, the radius cell, and the initial angle cell.  Everything else follows from these values.  A few notes are in order:

1. The polygon that is determined, is inscribed inside of the circle with the given radius, and centered around the origin. 
2. All angles are specified and calculated in radian measure.
3. If fewer than 50 vertices are needed, the rows will repeat.
4. If you wanted the center somewhere other than the origin, just apply a translation to the points.  So, if you want center (a, b), then each point P = (x, y), becomes P' = (x + a, y + b).  If you've made it this far into this post, you are probably more than capable.

Why Try to Reduce Calls to Trig Functions?

As the user of calculation software and scientific calculators, you may be wondering why we would want to reduce our use of trig functions.  The main reason would be for time-critical applications.  This particular spreadsheet is obviously not one of those, but it demonstrates the accuracy of the method.  So, how do I know that trigonometric functions take a long time to perform.  First of all, let me debunk some myths:

1. Computers and calculators have tables of numbers in them that they use to determine values of "complicated" functions.  So wrong!  Computers and calculators compute/calculate these values!
2. The calculations that computers and calculators do are just based on tables and interpolation.  This is rarely true.  Sometimes a programmer will use a method like this when he knows that the precision needs of his application will be met this way and will be much faster.  But it is actually more programming effort and would only be done when you didn't need very accurate results but you needed them really, really fast.
3. Computers and calculators have hardware circuits that make the complex calculations almost as fast as the simple ones.  Not so.  Fact:  Multiplication is done with the fmult instruction.  Addition is done with the fadd instruction.  fmult takes way, way more computer cycles to compute than fadd.  fsincos takes way, way longer than fmult.  It is an unavoidable consequence of the nature of these calculations.

Recall that multiplication is dependant on addition.  Several additions actually.  So it should come as no surprise that by the time you put together a circuit that does the job that several additions and small multiplications can do, you end up with a circuit that takes longer to complete than one that just does addition.

The same is true of trig functions.  You know how you calculate them?  Here are the magic formulas:

The dots (...) indicate that it goes on and on and on and on and on, until the changes are small enough that you aren't changing the digits that mater to you. You may need more terms than are listed to get the accuracy you need. These formulas above are not written in the most computationally efficient manner, but you can rest assured that any circuitry or coding or combination thereof, which computes the values of the above functions will take longer than 4 multiplications and 2 addition/subtractions will (those are the operations involved in doing vector rotation).

Enter Vector Rotation

The key to how this method helps us, is that we can use a few trig function calls at the beginning and reuse the results several times over. We compute the direction vector for the central angle, θ, that each side covers. For a hexagon, this angle is 360°/6 = 60°, or π/3.

We need to determine the value of the central angle using direct calls to trig functions, but we will be able to reuse those values.  We also call trig functions to get our initial position.  From there we use our vector rotation method.  So, E14 and F14 use the values in E11 and F11 (renamed mx and my) and those of E13 and F13 to find their values:

E14 =E13*mx-F13*my

F14 =E13*my+F13*mx

Cells in rows below 14 do the same thing.  They still reference mx and my, which are the cosine and sine of our central angle, θ, respectively, and they reference the cells directly above them.  The concept for each row is:  rotate the point in the row above me around the origin by the central angle and tell me the x and y values for that rotated point.

Proof of the Formulas

Suppose we are given a point (x, y) and denote the distance from the origin as r and the angle it makes with the positive axis as i.  We wish to rotate (x, y) counter-clockwise about the origin by angle θ.  The diagram below illustrates:

Our new point (x', y') can be simplified:

                  

                      
                      
                 
                     
                     

If you look back at the formulas for E14 and F14, you may observe that mx and my correspond with sin θ and cos θ and E13 and F13 correspond with x and y.  That's all there is to it. 

Relationship with Complex Number Multiplication

If we represent the new point (x', y') as x' + y'j (where j is used to indicate the square root of -1), we can say:

This will produce an equivalent result to what we have above.