Sum of Powers

In the sum of powers problem, we are looking for the sum of the p^th power of the first n integers. In this post, we consider the problem of determining a polynomial expression in n for a given power. The best known case is for p = 1, namely,

More generally, we should like a formula for a polynomial f_p such that

We will begin by defining a function and proceed to prove that it satisfies the above equality. We define:

Proposition 1. For all real numbers $n$ and natural numbers $p$,

Proof:  First we observe that (n + 1) – n = 1 = (n + 1)⁰, so that we have our induction base set. Suppose that for any real number n > 0 and a given natural number p we have,

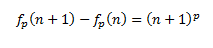
Now, given any real number n > 0,

which completes the argument.■

Proposition 2. For all natural numbers $n$ and $p$

$$f_p(n) = \sum_{i=1}^n{i^p}$$

Proof: First we see from the definition both that $f_0(1) = 1$ and, for any $p > 1$

$$f_{p}(1) = p \Big(\int_0^1 f_{p-1}(x) \mathrm{d}x - 1 \int_0^1 f_{p-1}(x) \mathrm{d}x\Big) + 1 = 1,$$

which establishes $1 \in S$. Suppose that $n \in S$. Then

$$f_p(n) = \sum_{i=1}^n{i^p},$$

and from proposition 1

$$f_p(n+1) - f_p(n) = (n + 1)^p$$

which rearranges to

$$f_p(n+1) = f_p(n) + (n+1)^p$$

$$= \sum_{i=1}^n{i^p} + (n+1)^p  = \sum_{i=1}^{n+1}{i^p}$$

■

The formula we have given for f_p allows us to calculate the first p sum of powers polynomials in time O(p²) which is a big improvement when compared to solving a system of linear equations to find the largest of them, which would require time O(p³) (to find all of them using a system of linear equations requires O(p⁴)).

The following Maxima program and its output, gives a demonstration of how to implement the above formula:
f[0]: n$ for p: 1 thru 100 do ( f[p]: integrate(expand(p*f[p-1]),n), C: 1 - ev(subst([n=1],f[p])), f[p]: f[p] + n*C )$ [f[0],f[1],f[2],f[3],f[4],f[5]];

[n,n^2/2+n/2,n^3/3+n^2/2+n/6,n^4/4+n^3/2+n^2/4,n^5/5+n^4/2+n^3/3-n/30,n^6/6+n^5/2+(5*n^4)/12-n^2/12]